Se consideră un circuit 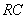 serie, alimentat de la o sursă de tensiune alternativă sinusoidală, a cărei tensiune este descrisă de expresia
serie, alimentat de la o sursă de tensiune alternativă sinusoidală, a cărei tensiune este descrisă de expresia 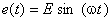 .
.
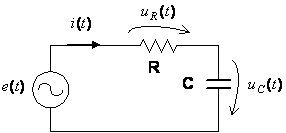
Figura 4 - Schema circuitului RC serie
Cunoscând valorile lui 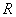 şi
şi 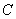 , se cere să se determine, în regim permanent, evoluţia în timp a curentului din circuit,
, se cere să se determine, în regim permanent, evoluţia în timp a curentului din circuit, 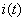 , tensiunea la bornele rezistorului,
, tensiunea la bornele rezistorului, 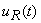 şi la bornele condensatorului,
şi la bornele condensatorului, 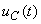 .
.
Aplicând Teorema a II-a a lui Kirchhoff, suma tensiunilor la bornele rezistorului şi condensatorului, este egală cu tensiunea sursei:
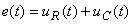
Utilizând amplitudini complexe, relaţia de mai sus se scrie:
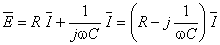
în care 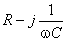 reprezintă impedanţa complexă a rezistenţei înseriate cu condensatorul.
reprezintă impedanţa complexă a rezistenţei înseriate cu condensatorul.
Explicitând 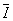 din expresia anterioară, se obţine:
din expresia anterioară, se obţine:
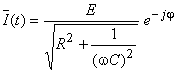 |
cu |
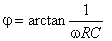 |
şi |
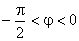 |
Diagrama fazorială a impedanţelor, amplitudinilor complexe ale tensiunii sursei şi curentului, este reprezentată în figura următoare.
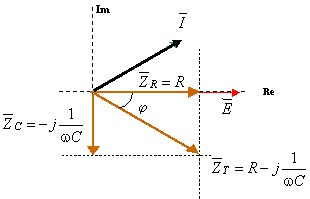
Figura 5 - Diagrama fazorială
Având calculat curentul, se pot calcula imediat tensiunile la bornele celor două elemente:
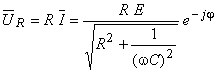
Amplitudinea complexă 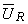 este colineară cu
este colineară cu 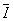 , ceea ce înseamnă că tensiunea la bornele rezistorului şi curentul ce îl străbate, sunt în fază.
, ceea ce înseamnă că tensiunea la bornele rezistorului şi curentul ce îl străbate, sunt în fază.
În ceea ce priveşte tensiunea la bornele condensatorului, se obţine:
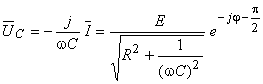
Amplitudinea complexă 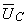 este în urmă cu
este în urmă cu 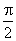 faţă de
faţă de 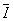 , ceea ce înseamnă că tensiunea la bornele condensatorului este în urmă cu
, ceea ce înseamnă că tensiunea la bornele condensatorului este în urmă cu 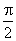 faţă de curentul ce îl parcurge.
faţă de curentul ce îl parcurge.
Diagrama fazorială completă a tensiunilor şi curentului din circuit este reprezentată în figura următoare, în care se evidenţiază Teorema a II-a a lui Kirchhoff: suma fazorilor 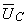 şi
şi 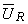 este egală cu fazorul
este egală cu fazorul 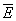 .
.
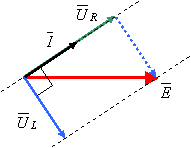
Figura 6 - Diagrama fazorială a circuitului RC serie
Pentru a obţine expresiile evoluţiilor în timp ale mărimilor, trebuie să se determine fazorii rotitori corespunzători (multiplicarea amplitudinilor complexe cu 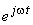 ) şi să se proiecteze pe axa imaginară.
) şi să se proiecteze pe axa imaginară.
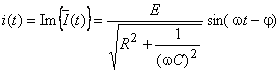

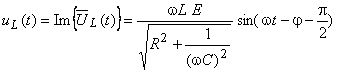
cu |
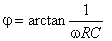 |
şi |
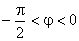 |
Expresiile de mai sus au fost obţinute considerând că tensiune ce alimentează circuitul are faza iniţială nulă. Ca exerciţiu, să se rezolve acelaşi circuit RC serie, considerând că faza iniţială a curentului din circuit, este nulă, respectiv, 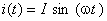 , curent reprezentat de amplitudinea complexă
, curent reprezentat de amplitudinea complexă 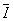 .
.
Amplitudinea complexă 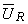 , care reprezintă tensiunea la bornele rezistorului, este colineară cu
, care reprezintă tensiunea la bornele rezistorului, este colineară cu 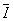 , ceea ce înseamnă că tensiunea la borne şi curentul aferente unui rezistor, sunt în fază.
, ceea ce înseamnă că tensiunea la borne şi curentul aferente unui rezistor, sunt în fază.
În ceea ce priveşte amplitudinea complexă 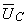 , ce reprezintă tensiunea la bornele condensatorului, ea este în urmă cu
, ce reprezintă tensiunea la bornele condensatorului, ea este în urmă cu 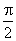 faţă de
faţă de 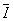 , ceea ce înseamnă că tensiunea la bornele unui condensator este în urmă cu
, ceea ce înseamnă că tensiunea la bornele unui condensator este în urmă cu 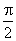 faţă de curentul ce îl parcurge.
faţă de curentul ce îl parcurge.
În final, diagramele vectorială şi temporală ce se obţin, sunt perfect echivalente cu cele corespunzătoare considerării tensiunii cu fază iniţială nulă; diferă doar momentul la care ne referim.