Utilizând notaţia în complex şi considerând că fazorul rotitor al curentului care parcurge unul din elemente este reprezentat de expresia:
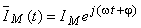 ,
,
în secţiunea anterioară, s-au obţinut următoarele expresii pentru fazorii rotitori ai tensiunilor, pentru rezistor, inductanţă, respectiv condensator:
Rezistor |
Inductanţă |
Condensator |
|
|
|
Ţinând cont de expresia lui 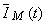 , expresiile de mai sus pot fi scrise sub forma:
, expresiile de mai sus pot fi scrise sub forma:
Rezistor |
Inductanţă |
Condensator |
|
|
|
Se defineşte impedanţa complexă, 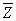 , ca fiind raportul dintre fazorii rotitori ai tensiunii şi curentului:
, ca fiind raportul dintre fazorii rotitori ai tensiunii şi curentului:
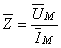
Explicitând impedanţa complexă în cazul elementelor R, L şi C, se obţin:
Rezistor |
Inductanţă |
Condensator |
|
|
|
Impedanţa complexă se exprimă în Ohm 
Amplitudinile şi impedanţele complexe pot fi reprezentate fazorial, pentru fiecare din elementele analizate.
Rezistor |
Inductanţă |
Condensator |
|
|
|
De notat faptul că impedanţa complexă este un fazor rotitor, fiind reprezentată ca orice mărime alternativă sinusoidală.
Aceasta se justifică, deoarece impedanţa inductanţelor şi condensatoarelor se modifică în funcţie de frecvenţa tensiunii de alimentare a circuitului, spre deosebire de impedanţa unei rezistenţe, care rămâne constantă ca valoare.
Deoarece tensiunea la borne şi curentul sunt alternative, de aceeaşi pulsaţie 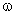 , termenul
, termenul 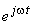 se poate neglija în scrierea ecuaţiilor caracteristice ale elementelor, sub formă fazorială, simplificându-se astfel notaţia. În ecuaţiile astfel scrise, nu mai apar termeni fazori rotitori, ci doar amplitudini complexe, ceea ce corespunde reprezentării fazorului rotitor la momentul
se poate neglija în scrierea ecuaţiilor caracteristice ale elementelor, sub formă fazorială, simplificându-se astfel notaţia. În ecuaţiile astfel scrise, nu mai apar termeni fazori rotitori, ci doar amplitudini complexe, ceea ce corespunde reprezentării fazorului rotitor la momentul 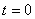 .
.
Rezistor |
Inductanţă |
Condensator |
|
|
|