REZISTOR

Se consideră un rezistor, pentru care sensurile de referinţă ale tensiunii şi curentului sunt cele reprezentate în figura următoare.

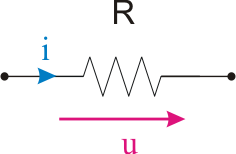
Considerând că rezistorul este parcurs de un curent alternativ sinusoidal, a cărui expresie este:

,

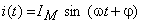aplicând ecuaţia caracteristică a rezistenţelor, 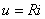, se poate determina tensiunea între bornele sale:

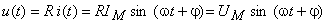
Rezultă că tensiunea între bornele unui rezistor este o mărime alternativă sinusoidală, de pulsaţie 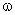, care este în fază cu curentul 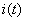şi care are amplitudinea egală cu .

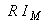În notaţie complexă, fazorul rotitor ce reprezintă curentul 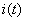este:

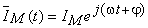
şi, pe baza ecuaţiei caracteristice, fazorul rotitor al tensiunii, 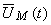, va fi:

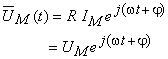
Fazorul rotitor al tensiunii va avea aceeaşi viteză unghiulară ca şi 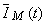şi este coliniar cu acesta; evoluţia în timp a tensiunii 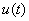se obţine proiectând acest fazor pe axa imaginară.

Doar pentru un rezistor, tensiunea la bornele sale şi curentul ce îl parcurge, sunt în fază.

În figura următoare este reprezentată evoluţia temporală şi diagrama fazorială a tensiunii la borne şi curentului în cazul unui rezistor.

 

INDUCTANŢĂ

Se consideră o inductanţă, pentru care sensurile de referinţă ale tensiunii şi curentului sunt cele reprezentate în figura următoare.

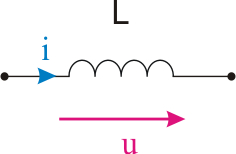
Considerând că inductanţa este parcursă de un curent alternativ sinusoidal, a cărui expresie este:

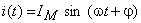
aplicând ecuaţia caracteristică a inductanţelor, 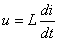se poate determina tensiunea între bornele sale:

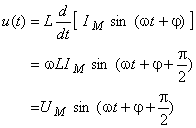
Rezultă că tensiunea între bornele unei inductanţe este o mărime alternativă sinusoidală, de pulsaţie 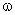, care este în avans cu 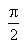faţă de curentul 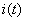şi care are amplitudinea egală cu .

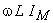În notaţie complexă, fazorul rotitor ce reprezintă curentul 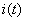este:

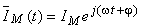
şi, pe baza ecuaţiei caracteristice, fazorul rotitor al tensiunii, 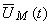va fi:

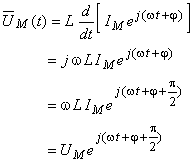
Fazorul rotitor al tensiunii va avea aceeaşi viteză unghiulară ca şi 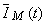, fiind în avans cu 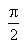faţă de acesta; evoluţia în timp a tensiunii 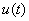se obţine proiectând acest fazor pe axa imaginară.

În figura următoare este reprezentată evoluţia temporală şi diagrama fazorială a tensiunii la borne şi curentului în cazul unei inductanţe.

 

CONDENSATOR

Se consideră un condensator, pentru care sensurile de referinţă ale tensiunii şi curentului sunt cele reprezentate în figura următoare.

Considerând că acesta este parcurs de un curent alternativ sinusoidal, a cărui expresie este:

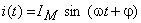
aplicând ecuaţia caracteristică a condensatoarelor, 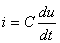se poate determina tensiunea între bornele sale:

Rezultă că tensiunea între bornele unui condensator este o mărime alternativă sinusoidală, de pulsaţie 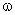, care este în urmă cu 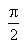faţă de curentul 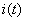şi care are amplitudinea egală cu .

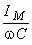În notaţie complexă, fazorul rotitor ce reprezintă curentul 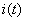este:

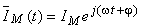
şi, pe baza ecuaţiei caracteristice, fazorul rotitor al tensiunii, 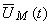va fi:

Fazorul rotitor al tensiunii va avea aceeaşi viteză unghiulară ca şi 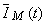fiind în avans cu 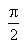faţă de acesta; evoluţia în timp a tensiunii 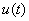se obţine proiectând acest fazor pe axa imaginară.

În figura următoare este reprezentată evoluţia temporală şi diagrama fazorială a tensiunii la borne şi curentului în cazul unui condensator.