Conform Teoremei a II-a a lui Kirchoff (Legii ochiurilor), în orice moment, suma algebrică a tensiunilor de-a lungul oricărui ochi de circuit, este nulă.

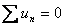
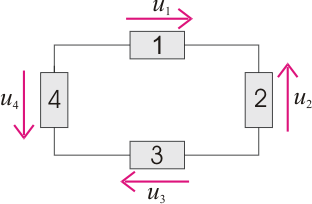
Figura 6 – Explicativă pentru Teorema a II-a (Legea ochiurilor)

Cu sensurile de referinţă specificate în figura de mai sus şi parcurgând ochiul în sensul acelor de ceasornic, Teorema a II-a a lui Kirchhoff conduce la ecuaţia:

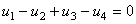
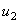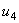De notat faptul că, tensiunile şi au fost considerate cu semn negativ, deoarece sensurile lor de referinţă, sunt opuse sensului de parcurgere a ochiului. Indiferent de sensul de parcurgere a ochiului (în sens orar sau trigonometric), se vor obţine ecuaţii de tensiuni absolut echivalente.

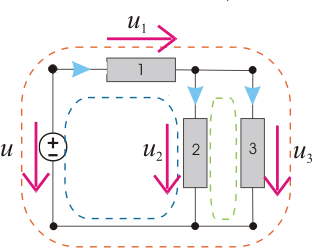
Figura 7 – Ochiurile circuitului

Faptul că suma tensiunilor de-a lungul ochiului este nulă, este echivalent cu a spune că lucrul necesar dislocării sarcinii în lungul ochiului, este nul. Din acest motiv, se poate considera că sistemul este conservativ.

Pentru circuitul din Figura 7, aplicarea Teoremei a II-a a lui Kirchhoff, conduce la:

• pe ochiul indicat cu linie roşie, parcurs în sens orar u₁ + u₃ - u = 0
• pe ochiul indicat cu linie albastră, parcurs în sens orar u₁ + u₂ - u = 0
• pe ochiul indicat cu linie verde, parcurs în sens orar u₃ - u₂ = 0

Din cele 3 ecuaţii, doar două sunt liniar independente.

Generalizând pentru M ochiuri de circuit, Teorema a II-a a lui Kirchhoff permite obţinerea a 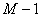ecuaţii liniar independente.

Ultima ecuaţie ne permite să afirmăm că, tensiunea între bornele elementului 2 este egală cu cea dintre bornele elementului 3; cu alte cuvinte, tensiunile între bornele celor două elemente, sunt identice. În această situaţie, se spune despre cele două elemente că sunt conectate în paralel.