Chiar dacă se cunosc toate elementele ce formează un circuit şi ecuaţiile caracteristice corespunzătoare, (Componente elementare), nu este posibil să se determine totalitatea tensiunilor şi curenţilor din circuit. Este necesar să se cunoască cele două teoreme importante, cunoscute ca Teoremele lui Kirchhoff.

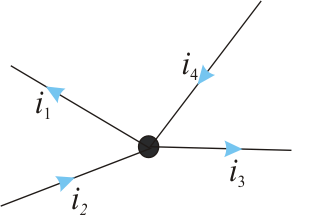
Figura 4 – Explicativă pentru Teorema I (Legea nodurilor)

Conform Teoremei I, în orice moment, suma algebrică a curenţilor ce intră sau ies dintr-un nod, este nulă.

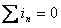
Pentru curenţii reprezentaţi în Figura 4, Teorema I conduce la ecuaţia:

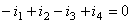
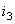De notat faptul că şi s-au considerat cu semn negativ, deoarece, s-a ales acelaşi sens de referinţă pentru curenţii care intră şi ies din nod. Cu alte cuvinte, suma curenţilor care "intră" în nod este egală cu suma celor ce "ies" din nod.

Astfel, dacă suma curenţilor ce intră în nod este egală cu suma celor ce ies, nodul nu poate acumula sarcină electrică. Altfel spus, un nod este perfect conductor, fără posibilitatea acumulării de sarcină electrică.

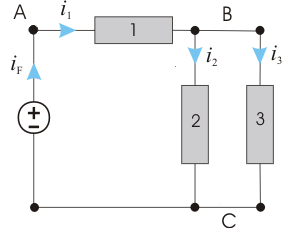
Figura 5 – Curenţii din circuit

Pentru circuitul reprezentat în figura de mai sus, aplicarea Teoremei I conduce la:

• în nodul A
• în nodul B
• în nodul C

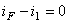
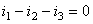
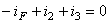
Dintre aceste 3 ecuaţii, doar două sunt liniar independente.

Generalizând pentru un circuit cu N noduri, Teorema I a lui Kirchhoff, permite obţinerea a 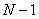ecuaţii liniar independente.

Prima ecuaţie ne permite să afirmăm că i_F, curentul ce iese din sursă, este egal cu cel care intră în elementul 1; cu alte cuvinte, sursa şi elementul 1 sunt parcurse de acelaşi curent. În această situaţie, se spune că sursa şi elementul 1 sunt conectate în serie.