Pentru anumite circuite mai complexe, este mai simplu să se utilizeze echivaleţele asocierii rezistoarelor în serie (vezi Teorema I a lui Kirchhoff) şi în paralel (vezi Teorema a II-a a lui Kirchhoff), decât să se recurgă la aplicarea metodei generale.

 

Rezistoare în serie

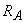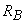Se consideră o porţiune de circuit formată din două rezistoare şi conectate în serie, reprezentată în figura de mai jos.

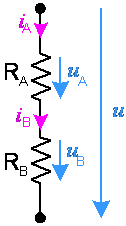
Figura 2 - Rezistoare în serie; divizor de tensiune

Cunoscând tensiunea 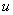la bornele elementelor înseriate, cum se repartizează aceasta între cele două rezistoare?

Prin aplicarea teoremei a II-a a lui Kirchhoff se obţine:

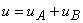
Ţinând cont de ecuaţiile caracteristice ale fiecărui rezistor, rezultă:

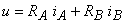
Aplicând teorema I a lui Kirchhoff se obţine 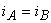, respectiv:

ceea ce ne permite să afirmăm că două rezistoare în serie sunt echivalente cu un rezistor, a cărui rezistenţă este egală cu suma rezistenţelor celor două rezistoare înseriate.

Expresia (1) este echivalentă cu:

,

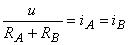ceea ce ne permite să concluzionăm că tensiunile la bornele fiecărui rezistor vor fi :

Raţionamentul de mai sus se poate generaliza pentru 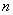rezistoare conectate în serie, respectiv, tensiunea la bornele rezistorului 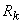este:

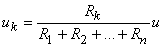
Asocierea de rezistoare prezentată în Figura 2 se numeşte divizor de tensiune, deoarece tensiunea 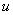dintre bornele conexiunii serie, se divide în mai multe tensiuni, la bornele rezistoarelor înseriate.

 

Rezistoare în paralel

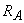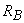Se consideră o porţiune de circuit formată din două rezistoare şi conectate în paralel, reprezentată în figura de mai jos.

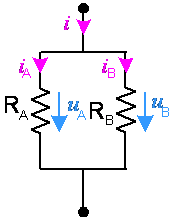
Figura 3 - Rezistoare în paralel; divizor de curent

Cunoscând curentul 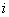care circulă prin acest ansamblu în paralel, cum se repartizează acesta între cele două rezistoare?

Aplicând teorema I a lui Kirchhoff se obţine:

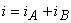
Ţinând cont de ecuaţiile caracteristice ale celor două rezistoare rezultă:

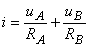
Aplicând teorema a II-a a lui Kirchhoff se obţine 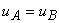, respectiv:

ceea ce este echivalent cu

,

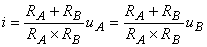ceea ce ne permite să afirmăm că două rezistoare în paralel sunt echivalente cu un rezistor, a cărui invers al rezistenţei este egal cu suma inverselor rezistenţelor celor două rezistoare în paralel.

Expresia (2) este echivalentă cu:

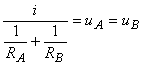
ceea ce ne permite să concluzionăm că prin fiecare rezistor vor circula curenţii:

Raţionamentul de mai sus se poate generaliza pentru 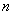rezistoare conectate în paralel, respectiv curentul prin rezistorul 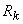este:

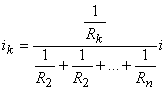
Asocierea de rezistoare prezentată în Figura 3 se numeşte divizor de curent, deoarece curentul 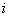care circulă prin ansamblul de rezistoare, se divide în curenţii care circulă prin fiecare rezistor conectat în paralel.