Metoda generală de rezolvare a unui circuit constă în scrierea şi rezolvarea unui sistem de ecuaţii ce reprezintă legăturile dintre tensiunile şi curenţii din circuit. Aceste ecuaţii se obţin atât pe baza teoremelor lui Kirchhoff, cât şi prin scrierea ecuaţiilor caracteristice ale elementelor din circuit (Componente elementare). În această secţiune se vor considera doar circuitele rezistive, respectiv care nu conţin inductanţe sau capacităţi.
În continuare se va aplica următoarea metodă:
• Se vor numerota cele 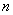 elemente (surse şi rezistenţe) din circuit. Cum fiecărui element i se asociază o tensiune şi un curent, celor elemente (surse şi rezistenţe) din circuit. Cum fiecărui element i se asociază o tensiune şi un curent, celor 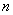 elemente le corespund elemente le corespund 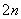 necunoscute ce trebuie determinate, respectiv, sunt necesare necunoscute ce trebuie determinate, respectiv, sunt necesare 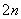 ecuaţii linear independente. ecuaţii linear independente. |
|
• Se scriu cele 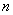 ecuaţii caracteristice corespunzătoare celor ecuaţii caracteristice corespunzătoare celor 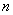 elemente din circuit (Componente elementare) elemente din circuit (Componente elementare) |
|
• Se vor numerota cele 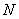 noduri din circuit şi se vor scrie noduri din circuit şi se vor scrie 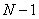 ecuaţii linear independente care rezultă din aplicarea Teoremei I a lui Kirchhoff. ecuaţii linear independente care rezultă din aplicarea Teoremei I a lui Kirchhoff. |
|
• Se poate demonstra că numărul 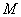 de ecuaţii linear independente ce rezultă prin aplicarea Teoremei a II-a a lui Kirchhoff, depinde de numărul de elemente şi de noduri prin relaţia de ecuaţii linear independente ce rezultă prin aplicarea Teoremei a II-a a lui Kirchhoff, depinde de numărul de elemente şi de noduri prin relaţia 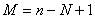 . . |
|
• În final, se rezolvă sistemul obţinut de 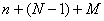 ecuaţii. ecuaţii. |
Sistemul este format din:
|
|
|
|
|
|
|
|
|
ecuaţii linear independente, deci, suficiente pentru determinarea celor 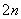 necunoscute.
necunoscute.
Se consideră circuitul din Figura 1:
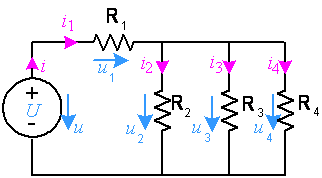
Figura 1 - Exemplu de circuit
• În acest circuit există 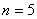 elemente (4 rezistenţe şi o sursă de tensiune) ceea ce înseamnă că avem
elemente (4 rezistenţe şi o sursă de tensiune) ceea ce înseamnă că avem 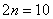 necunoscute de determinat: 5 tensiuni (
necunoscute de determinat: 5 tensiuni (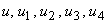 ) şi 5 curenţi (
) şi 5 curenţi (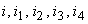 ).
).
• Cele 5 ecuaţii caracteristice ale elementelor sunt:
|
|
|
|
|
• Există 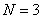 noduri în circuit, respectiv se pot scrie
noduri în circuit, respectiv se pot scrie 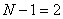 ecuaţii linear independente prin aplicarea teoremei I a lui Kirchhoff:
ecuaţii linear independente prin aplicarea teoremei I a lui Kirchhoff:
|
|
• Există 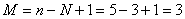 ecuaţii linear independente ce rezultă prin aplicarea teoremei a II-a a lui Kirchhoff. Una din combinaţiile de 3 ecuaţii este:
ecuaţii linear independente ce rezultă prin aplicarea teoremei a II-a a lui Kirchhoff. Una din combinaţiile de 3 ecuaţii este:
|
|
|
Dar se poate considera şi:
|
|
|