Comanda vectorială a maşinii asincrone
3.3 Elemente pregătitoare
Tensiunile, curenţii şi fluxurile trifazate ale maşinilor de c.a. pot fi reprezentate prin vectori spaţiali (denumiţi şi sinori, vectori spaţio-temporal reprezentativi).
În cele ce urmează se va considera cazul curenţilor statorici pentru care valorile instantanee pe axele a, b si c sunt ia, ib, ic.
Vectorul spaţial ![]() descrie ansambulul
descrie ansambulul ![]() şi este dat de - fig. 1:
şi este dat de - fig. 1:
(2). |
Cei mai mulţi autori iau pentru k valorea 2/3. Această alegere (necritică) este justificată de o transformare inversă a tensiunii magnetomotoare a unui sistem trifazat la valoarea corespunzătore de pe o fază (![]() ).
).
Fig. 1 Imaginea vectorului spaţial pentru curentul statoric
Pentru a transforma sitemul trifazat variabil într-un sistem bifazat invariabil (ca al motorului de c.c) se fac transformările următoare:
Vectorul spaţial este raportat la un sistem de referinţă cu doua axe: a si b, a este ales având aceeaşi direcţie cu a.
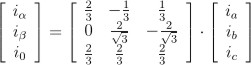
i0: componenta homopolară a sistemului. Când i0 = 0 (sau neglijabil), transformarea devine:
;

Această transformare - fig.3, face trecerea de la sistemul de axe (a, b) raportat la stator la un referenţial ortogonal (d,q) rotitor. Axa d este aleasă în aceeaşi direcţie cu fluxul rotoric. q dă pozitia acestui flux.
Fig. 3 Transformarea (a, b) ® (d, q)
Când se cunoaşte poziţia q a fluxului, se poate considera id şi iq ca valori «continui», deci, ca urmare a transformarilor Clarke si Park, sistemul a devenit invariabil într-un referenţial bifazat ataşat rotorului.
! Transformările Clarke şi Park pot fi aplicate printr-o relaţie combinată.
Transformările inverse: