1. Calculul câmpului
|
Se vor însuma câmpurile create de fiecare din cele m bobine. |
Câmpul H este o funcţie pară. |
|
2. Calculul armonicilor spaţiale |
|
Pentru a calcula armonicile spaţiale, se vor însuma armonicile de acelaşi rang, ale câmpurilor create de fiecare dintre înfăşurări.
Deoarece câmpul H este o funcţie pară, expresia generală a armonicii spaţiale de rang n, a câmpului creat de cele m bobine este:
pentru  i: i:

în care:
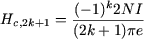
este coeficientul armonicii de rang 2k+1, a câmpului pe care cele N spire le-ar fi creat dacă ele ar fi fost concentrate în două crestături diametral opuse.
Construirea geometrică a coeficientului Hn
Construcţia geometrică ce permite determinarea coeficienţilor Hn ai armonicilor impare, este similară celei utilizate în cazul în a două bobine. Ea se bazează, de asemenea, pe valoarea obţinută prin expresia (1), calculată pentru q = 0. |
|
|
Armonicile Hn de rang impar, se pot exprima:
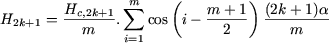
|
(2) |
|
- În cazul particular m = 3, există relaţia:

- H3 se anulează pentru: cos
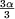 = - = - 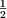  a = a = 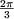 (a = 120°) (a = 120°)
- H5 se anulează pentru: cos
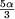 = - = - 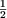  a = a =  (a = 72°) (a = 72°)
|
|
- În cazul particular m = 4, există relaţia:
Se verifică, o dată în plus, că armonica de rang 3 se anulează pentru a = 120°, în timp ce armonica de rang 5 se anulează pentru a = 72°. |
|
| Este de aşteptat ca acest rezultat să se obţină pentru un număr m oarecare de bobine. Suma (2) poate fi evaluată din considerente geometrice.
H2k+1 este reprezentat în figura 1, prin vectorul 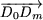 , ce este suma vectorilor , ce este suma vectorilor 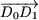 , ,  ,..., ,...,  , ,
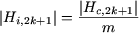
- defazajul unuia faţă de altul este de n.b =
 . .
|
|
|
|
|
|
Punctele D0 până la Dm se află pe un cerc cu centrul O, de rază OD0 (figura 2). Punctele O, Di-1, Di, i = 1, 2, ¼, m formează un triunghi isoscel, cu unghiul la bază g şi d în vârf. Se poate arăta (figura 2) că 2g+n.b = p.
Deoarece suma unghiurilor triunghiului este p, rezultă 2g+d = p, rezultă în final d = n.b. |
|
|
|
|
|
Lungimea razei OD0 este dată de (figura 3):
iar valoarea coardei D0Dm, de:
Rezultă în final:
sau, în funcţie de unghiul a de repartizare:
|
|
|
|
|
|
De asemenea, se verifică, pentru "m, că armonica de rang 3 se anulează pentru sin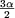 = 0, respectiv a = 120°, în vreme ce cea de rang 5 se anulează pentru a = 72° = 0, respectiv a = 120°, în vreme ce cea de rang 5 se anulează pentru a = 72° |
|
|