<< Întoarcere la răspuns | | Întoarcere la enunţ >>

Se poate compara pertinenţa ipotezelor considerate pentru calculul teoretic, prin compararea rezultatelor astfel obţinute (Figura 1), cu cele furnizate de modelarea cu elemente finite.
Figura 1: Rezultatul calculului teoretic
Această tehnică de calcul permite rezolvarea numerică a ecuaţiilor locale ale câmpului din maşină. Ea se bazează pe discretizarea spaţiului şi integrarea numerică a ecuaţiilor lui Maxwell.
Notă: Figurile 2 până la 6 au fost obţinute cu ajutorul programului FLUX2D, dezvoltat de firma Cedrat.
Figura 2: Secţiune prin maşina studiată	Se va considera maşina, ce are secţiunea transversală reprezentată în figura 2. Suprafeţele în albastru şi magenta corespund miezului statorului, respectiv rotorului. Acesta este realizat din tole din material feromagnetic, a cărui permeabilitate relativă este mare, atât timp cât nu se atinge nivelul de saturaţie. Zonele reprezentate cu bleu, corespund unor porţiuni ale spaţiului, care din punct de vedere magnetic, au aceleaşi proprietăţi ca şi aerul. Ele pot corespunde, fie într-adevăr aerului (cum ar fi întrefierul), fie unor conductoare de cupru prin care nu circulă curent (cazul crestăturilor din rotor şi ale majorităţii celor din stator), fie axului motorului (pe care îl presupunem realizat din oţel nemagnetic). În sfârşit, cele două suprafeţe, în roşu şi galben, reprezintă două crestături, ce conţin conductoare parcurse de curent.
Nu vom considera în acest studiu, fiecare conductor, cu secţiunea şi poziţia lui exactă (pe care, de altfel ar fi imposibil de determinat, ţinând cont de faptul că reprezintă un mănunchi), ci vom considera cele două crestături ca fiind zone ce conţin un material, ale cărui proprietăţi magnetice sunt apropiate de cele ale aerului şi parcurse de un curent, care determină densitatea de curent j constantă şi egală cu , în care N este numărul spirelor bobinei, I este curentul care circulă, S suprafaţa crestăturii, iar k coeficientul de umplere, care reprezintă raportul dintre aria totală a conductoarelor şi cea a crestăturii (k = , dacă notăm cu c, secţiunea unui conductor).
Figura 3: Divizarea în apropierea întrefierului	Suprafaţa studiată este divizată în aproximativ 6000 de elemente, a căror formă este cât mai apropiată de un triunghi echilateral, pentru a avea o bună divizare a spaţiului. Divizarea este mai fină în apropierea întrefierului (figura 3) şi mai largă în rest (zona axului sau partea exterioară a statorului, de exemplu), pentru a limita numărul de elemente. Acestor elemente le sunt asociate aproximativ 12000 de puncte (noduri), care corespund, fie vârfurilor triunghiurilor, fie mijloacelor laturilor. În fiecare din aceste puncte se va calcula potenţialul vector (definit de  =  ). Acesta, pentru o problemă bi-dimensională, ca cea de faţă, nu are decât o componentă nenulă A z, perpendiculară pe planul figurii.
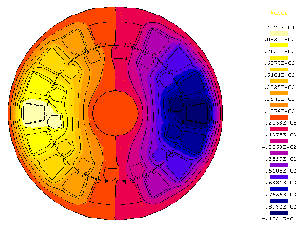
Figura 4: Valorile potenţialului vector	În figura 4 este reprezentată valoarea acestui potenţial în toate punctele secţiunii maşinii. Se observă că acesta este negativ în jurul crestăturii ce conţine conductoarele parcurse de curent în sensul "spre planul figurii" şi pozitiv pentru cealaltă crestătură. Liniile echipotenţiale ale potenţialului vector corespund traiectoriilor fluxului magnetic. Se observă că fluxul, înconjoară cele două crestături.
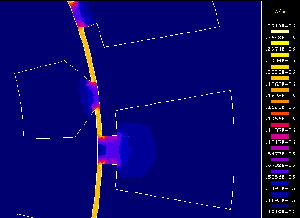Figura 5: Valoarea câmpului H	Dacă se urmăresc acum valorile câmpului H, se observă în figura 5, că valoare sa este cvasi-nulă peste tot, mai puţin în întrefier.
Figura 6: Reprezentarea vectorului H în întrefier	În figura 6 este reprezentat, sub formă vectorială, câmpul H, calculat în toate punctele aflate la mijlocul întrefierului. Se observă că această reprezentare este destul de apropiată de cea obţinută prin calculul analitic prezentat anterior (figura 1). Diferenţele sunt cauzate de existenţa crestăturilor, atât în rotor, cât şi în stator. Acestea determină deformarea locală a câmpului.

<< Întoarcere la răspuns | | Întoarcere la enunţ >>