Întrebarea 4.a:

Câmpul H se poate calcula folosind două metode:

1. fie se procedează ca mai înainte, respectiv se aplică Teorema lui Ampère pe contururi alese corespunzător pentru a calcula H în orice punct;
2. fie se consideră că, câmpul rezultant H, creat de cele două bobine, se poate calcula ca sumă a câmpurilor create de fiecare dintre ele.

1. Aplicarea Teoremei lui Ampère

Se pot considera două tipuri de contururi:

Primul înconjoară două crestături parcurse de curenţi de acelaşi sens (Figura 1). Aplicând Teorema lui Ampère, rezultă: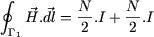

Figura 1

Cum:

• H este nul în fier şi radial în întrefier;
• din motive de simetrie, H(q ) = -H( p-q )

rezultă:   

,

sau:

Figura 2

În final se obţine:

Câmpul H este o funcţie pară.

2. Suma câmpurilor create de fiecare bobină

Se poate calcula câmpul total creat de cele două bobine, prin însumarea câmpurilor create de fiecare. Prima creează, în orice punct din întrefier, un câmp defazat cu -, a doua defazat cu +.

Întrebarea 4.b:

Şi în acest caz sunt posibile două metode:

1. fie calculul direct
2. fie însumarea componentelor armonice ale câmpurilor create de fiecare bobină

1. Calculul direct

Ca şi mai înainte, se calculează, ţinând cont de forma câmpului: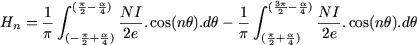

Se disting două cazuri:

• fie n este par (n = 2k), funcţia cos(2kq) având o perioadă de . Integrala acestei funcţii, calculată între (- +) şi ( -) este identică cu cea calculată între ( + ) şi ( - ).

  Rezultă că armonicile de rang par sunt nule.

• fie n este impar (n = 2k + 1), reultând:

2. Însumarea componentelor armonice ale câmpurilor create de fiecae bobină

Armonica de rang n a câmpului creat de cele două bobine este egal cu suma armonicilor de acelaşi rang, ale câmpurilor create de fiecare dintre bobine; deoarece câmpul H este o funcţie pară, rezultă:

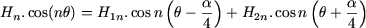
în care (pentru i = 1 sau i = 2):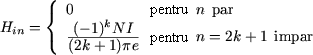

Rezultă imediat că armonicile H_n de rang par sunt nule.

Deoarece pentru q = 0,

(1),

rezultă coeficienţii Fourier ai armonicilor de rang impar: