Utilizând amplitudinile complexe ale tensiunii şi curentului dintr-un dipol, se defineşte puterea complexă, 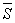 , ca fiind produsul dintre amplitudinea complexă a valorii efective a tensiunii şi complex-conjugatul amplitudinii complexe a valorii efective a curentului.
, ca fiind produsul dintre amplitudinea complexă a valorii efective a tensiunii şi complex-conjugatul amplitudinii complexe a valorii efective a curentului.
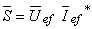 ,
,
în care 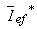 este complex-conjugatul lui
este complex-conjugatul lui 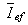 .
.
Ţinând cont că amplitudinile complexe sunt:
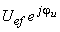 |
şi |
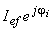 , , |
puterea complexă se scrie sub forma:
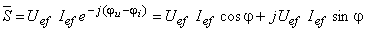 ,
,
unde 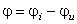 .
.
În expresia de mai sus, se poate identifica primul termen ca fiind puterea activă (sau reală), 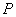 , definită anterior.
, definită anterior.
Prin analogie, se defineşte puterea reactivă (sau imaginară), ca fiind 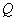 :
:
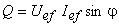 .
.
Unitatea de măsură a puterii reactive este volt-amper reactiv [VAR].
Astfel, puterea complexă poate fi scrisă sub forma:
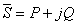 ,
,
şi reprezentată grafic prin aşa-numitul triunghi al puterilor, reprezentat în figura de mai jos.
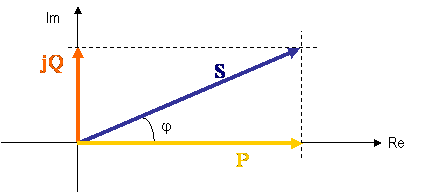
Figura 2 - Triunghiul puterilor
De observat că, atât puterea activă 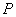 , cât şi puterea reactivă
, cât şi puterea reactivă 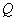 , iau doar valori reale; puterea complexă este exprimată însă prin numere complexe.
, iau doar valori reale; puterea complexă este exprimată însă prin numere complexe.
Este important de observat faptul că, puterile activă, reactivă şi complexă nu sunt fazori rotitori, deoarece evoluţiile lor în timp nu sunt sinusoidale; chiar dacă tensiunea şi curentul sunt sinusoidale (pot fi reprezentate prin fazori rotitori), puterile activă, reactivă şi complexă au valori constante (deci nu pot fi reprezentate prin fazori rotitori).
Modulul puterii complexe, 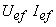 , se numeşte putere aparentă, se notează cu
, se numeşte putere aparentă, se notează cu 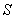 şi se exprimă în volt-amper [VA].
şi se exprimă în volt-amper [VA].
Factorul de putere, 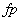 , se defineşte ca fiind raportul dintre puterile activă şi aparentă:
, se defineşte ca fiind raportul dintre puterile activă şi aparentă:
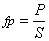 .
.
Factorul de putere este o mărime adimensională, iar în cazul regimului sinusoidal, el este numeric, identic egal cu 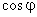 .
.
În tabelul următor se sintetizează expresiile diferitelor mărimi definite în această secţiune.
Puterea complexă |
|
|
- |
- |
Puterea aparentă |
|
|
volt-amper |
[VA] |
Puterea activă |
|
|
watt |
[W] |
Puterea reactivă |
|
|
volt-amper reactiv |
[VAR] |
Factor de putere |
|
|
- |
- |