Even if we know all the elements that form a circuit and the corresponding characteristic equations, (Basic Components), we can't determine all the voltages and currents from the circuit. It is necessary to know the two important laws, known as Kirchhoff's Laws.
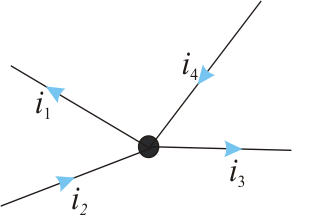
Figure 4 – Explanation for the 1st Law (The junction rule)
According to the 1st Law, for a given junction or node in a circuit, the algebraic sum of the currents entering or leaving a junction is zero.
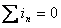
For the currents represented in Figure 4, the 1st Law leads to the equation:
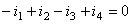
We have to note the fact that 
and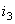 
have been considered with a negative sign, because the same reference direction has been chosen for the currents entering and leaving the junction. In other words, the sum of the currents "entering" the node equals the sum of the currents "leaving" the node.
Thus, if the sum of the currents entering the node equals the sum of the currents leaving the node, the node can not accumulate an electrical load. In other words, a junction is a perfect conductor, without the possibility of accumulating electrical load.
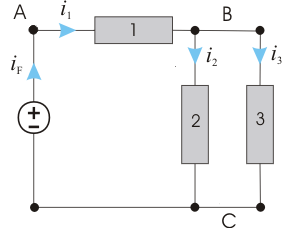
Figure 5 – The currents from the circuit
For the above represented circuit, applying the 1st Law leads to:
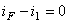
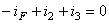
From these 3 equations, only two are linear independent.
Generalizing for a circuit with N junctions, the 1st Kirchhoff Law allows us to obtain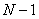 
linear independent equations.
The first equation allows us to declare that iF, the current that leaves the power supply, is equal to the current that enters in element 1; in other words, the power supply and the element 1 are traversed by the same current. In this situation, we say that the power supply and the element 1 are series connected.
