According to the 2^nd Kirchhoff Law (The loop rule), at any moment, the algebraic sum of the voltages around any closed loop, is zero.

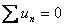
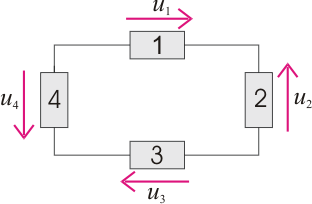
Figure 6 – Explanation for the 2^nd Law (The loop rule)

With the reference directions presented in the above figure and going around the loop clockwise, the 2^nd Kirchhoff Law leads to the equation:

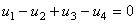
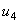We have to note the fact that the voltages and have been considered with a negative sign, because their reference directions are in opposition to the direction in which we chose to go around the loop. Regardless of the way we go around the loop (clockwise or counter-clockwise), equivalent voltage equations will be obtained.

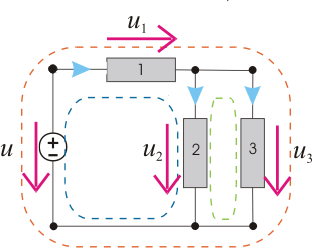
Figure 7 – The loops of the circuit

The fact that the sum of the voltages around a closed loop is zero is equivalent to saying that the energy necessary to dislocate the load along the loop is zero. We can therefore consider this law as a statement of energy conservation.

For the circuit in figure 7, applying the 2^nd Law leads to:

• for the red line indicated loop, going around in clockwise direction, u₁ + u₃ - u = 0
• for the blue line indicated loop, going around in clockwise direction, u₁ + u₂ - u = 0
• for the green line indicated loop, going around in clockwise direction u₃ - u₂ = 0

From the 3 equations, only two are linear independent.

Generalizing for a circuit with M loops, the 2^nd Kirchhoff Law allows us to obtain linear independent equations.

The last equation allows us to declare that the voltage between the terminals of element 2 is equal to the voltage between the terminals of element 3; in other words, the voltages between the terminals of the two elements, are the same. In this situation we say that the two elements are parallel connected.