A model is group of mathematical relationships which describes the behaviour of a system. Depending on the desired precision, we can use models that are more or less precise; there is therefore a compromise between the simplicity of the model and the desired representativness (precision).

In this course, most of the components from the circuits' structure will be considered as assimilated to some ideal elements, respectively voltage source and R, L and C elements previously studied.

In practice, models that express the reality more accurate are needed, real models of the components being necessary.

In practice, what happens if we short-circuit the terminals of a battery? The answer is that a very high current will be realized, and the battery will be "discharged" quickly, which means the annullement of the voltage at its terminals. This behaviour, verified in practice, cannot be described by using the model of the ideal voltage source previously presented, because the battery is a real voltage source and not an ideal one!

A more realistic model of a voltage source, consists of the series connection with an ideal voltage source, of a small resistance 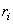, called intern resistance of the source, as we can see in the figure below:

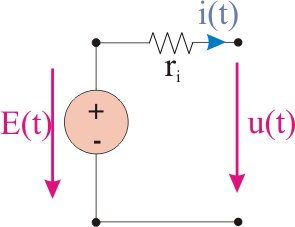
Figure 10 - Equivalent scheme of a voltage source

By applying Kirchhoff's 2^nd Law and the characteristic equation of a resistance, we obtain:

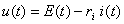
if we have a short-circuit at the terminals of the source, in the above expression we'll have , and the short-circuit current will be:

As the value of the resistance 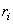is much smaller than the value of the electromotor voltage 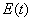, the short-circuit current will reach very high values, which can destroy the source.

The values of the parameters 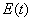, 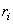and 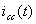characterize the source. If we know two of them, the 3^rd can be obtained.

Similar, a more realistic model o a current source, consists of a parallel connection with an ideal current source, of a high resistance 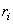, called intern resistance, as we can see in the figure below:

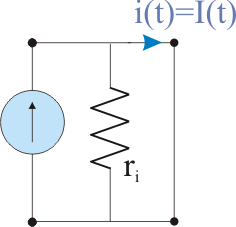
Figure 11 - Equivalent scheme of a current source

If the source is left in an open circuit, then 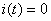, and the current will circulate between the source and the internal resistance, thus determining the voltage at the terminals of the source, :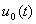

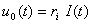
In practice, because of the designing technology, the biggest part of the resistances have a certain inductive behaviour, which means that the real model of a resistance is obtained by series connecting an ideal resistance with the value R ,with an inductance 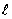, as seen in the figure below:

Figure 12- Equivalent scheme of a real resistance

An inductance is realized by a certain number of windings from conductive material, whose conductivity is very good; even so, because of the conductive material's resistivity, an inductance will also have a resistive character. A real model of an inductance is obtaied by series connecting the inductance L, with a small resistance 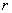, as seen in the figure below.

 

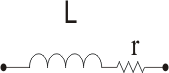
Figure 13 - Equivalent scheme of a real inductance

A "charged" capacitor (the voltage between its terminals is not zero), even if it isn't passed through by the current (open circuit), in time, will slowly "discharge" ( the voltage at the terminals reduces). This fact cannot be explained by means of the model previously presented. In practice, a real capacitor acts as an ideal capacity C, parallel connected with a high resistance R. The current that flows between the capacitor and this resistance, models the "discharging" phenomenon of the capacitor. This model is represented in the figure below.

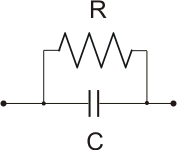
Figure 14- Equivalent scheme of a real capacitor

NOTE - The models presented are not unique; there have been considered the models that, in the context of this course, can explain the majority of the studied phenomenons. For special situations, or in order to obtain a higher precision, more complex models can be considered.