An ideal, independent current source is a dipole which has the capability to impose the current it provides, regardless of the voltage applied to its terminals.

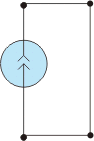
The symbol for representing a current source is:

There aren't any specific symbols for representing direct current sources (DC), respectively alternating current sources (AC).

The equation that characterizes an ideal current source is:

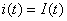
When we connect a current source with another passive element, we obtain a circuit in which the current 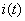flows.

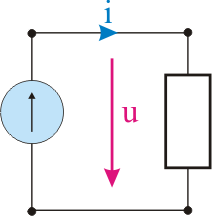
Figure 5 - Ideal current source supplying a passive element

The potential difference 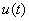between its terminals, depends on the element the source supplies:

• in the case of a current source, its terminals can be linked between them. In this case, the voltage 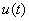between its terminals is zero and consequently the power it provides, 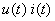, is zero;

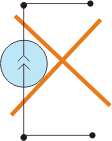
• a current source can never be left in an open circuit because this would correspond to the cancellation of the current it supplies; there must always be a circuit in which the current should flow; as a current source imposes 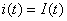, an open circuit imposes .

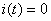• two current sources can be series connected if they have the same value of the current; thus, by using Kirchhoff's 1^st Law we obtain 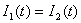, which is valid only if the two values of the current are equal.

 

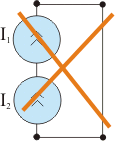Figure 6 - Ideal current source in short-circuit, in open circuit, and two current sources series connected.