In order to analyse the harmonic content of the output voltages we can start with the harmonic analysis of the potentials P_j of each of the arms.

Pseudo development in Fourier series of the potential P_j of an arm

We consider the case in which the potential P_j is determined by comparing the prescribed value P_jw and the reference voltage with the triangular wave form .

We suppose that the reference voltage has a unitary amplitude (=1) and the period T.

For P_j we have (figure 1)

Figure 1

• If would be constant (Figure 2), the potential would be a periodic function with the period T. Which would then be its development in Fourier series?

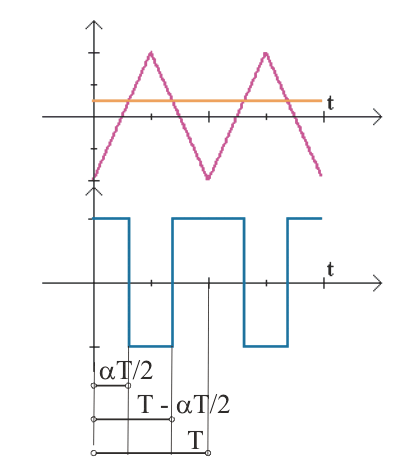
Figure 2

 

If varies in time, P_j is no longer a periodic function with the period T since the width of the pulses varies from period to period.

But if varies slowly in comparison to the modulation period T, the width of the pulses varies little from one modulation period to another: around one given moment t we can rebuild in a satisfactory manner , by considering the development in Fourier series which we would have had if had been a constant of value .

• How is the development in Fourier series modified in these conditions if ?

 

Analysis of the pseudo development in Fourier series

The pseudo development in Fourier series of P_j is

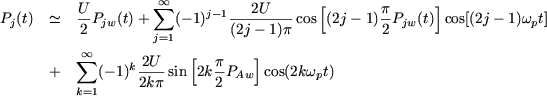Every component of this development has an "amplitude" that varies in time.

Thus, if , we have:

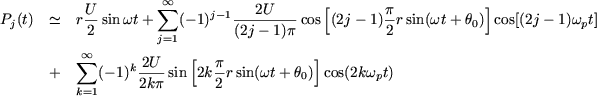· The "average value" of the potential P_j has the amplitude

It traces the reference value.

This confirms the affirmation that with a PWM command, the potential P_j traces, as an average value, its reference value .

· The pulsation term corresponding to the frequency of the reference voltage can be written:

• Prove that because of the variation in time of the "amplitude", instead of a pulsation harmonic line, there is a family of harmonic lines with , , ..., pulsations.