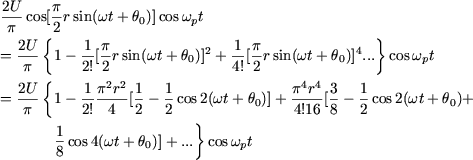 |
By regrouping the terms in ![]() ,
, ![]() ,
, ![]() , ... we have:
, ... we have:
 |
As ![]() , we finally obtain:
, we finally obtain:
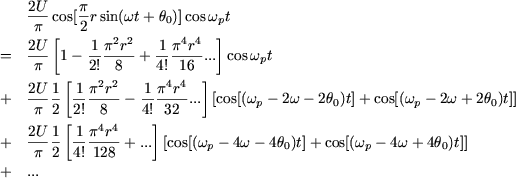 |
The ![]() pulsation and
pulsation and ![]() amplitude term is therefore the equivalent of the following set of harmonics:
amplitude term is therefore the equivalent of the following set of harmonics:
The amplitudes of the harmonics decrease rapidly as their pulsation pulls away from the pulsation wp.
· By a similar calculus, we can prove that the ![]() pulsation term of the pseudo development in Fourier series
pulsation term of the pseudo development in Fourier series
gives:
The harmonics group themselves in families situated around the pulsations ![]() ,
, ![]() ,
, ![]() ,...
,...