The average value of the potential Pj is equal to (figure 3)
 |
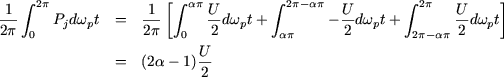Figure 3
Between 
and the potential 
we have the relation:
 |
respectively
 |
And therefore we have
 |
The development in Fourier series of the potential Pj only includes cosine terms because of the wave form's symmetry in relation to 
.
The first harmonic of Pj (the term in 
) has the amplitude (figure 4).
 |
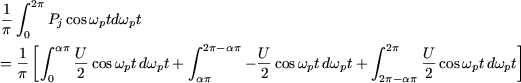Either
 |
As
 |
we finally have
 |
The second harmonic of PA (the term in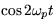 
) has the amplitude
 |
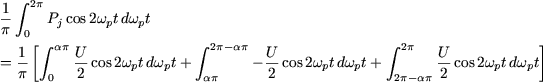Either
 |
As
 |
we finally have
 |
And so forth.
Figure 4
