Motorul este alimentat cu tensiunea nominală şi se înregistrează evoluţia vitezei pe durata opririi libere, determinată de deconectarea de la reţea (figura 11).

Figura 11

În continuare, se consideră originea timpului translatată în momentul t₀, respectiv t₀ = 0.

Momentul de inerţie J. Din ecuaţia generală a mişcării în momentul deconectării motorului

,

rezultă

.

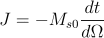Cuplul static în momentul deconectării M_s0 este datorat doar pierderilor mecanice,

,

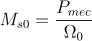iar raportul dt/dW se determină trasând tangenta la curba vitezei în momentul deconectării, rezultând

.

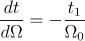În final, se obţine

,

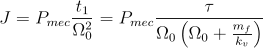întrucât

.

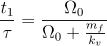Coeficientul de frecări vâscoase k_v. Deoarece în momentul deconectării

,

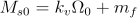se poate scrie

,

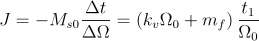respectiv

.

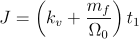(1)

Ecuaţia generală a mişcării pe durata opririi libere

,

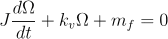are soluţia

,

cu

,

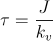(2)

constanta mecanică de timp.

Particularizând soluţia generală pentru t = t_s, W = 0, rezultă

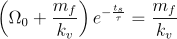, respectiv .

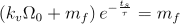Exprimând cuplul de frecări uscate m_f din (1),

,

(3)

ecuaţia de mai sus devine

.

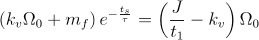Ţinând cont de (1) pentru exprimarea membrului drept al ecuaţiei de mai sus, se obţine:

.

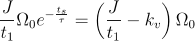Rezultă:

.

Ţinând cont şi de expresia constantei mecanice de timp (2), rezultă ecuaţia:

,

(4)

în care necunoscuta este k_v.

Ecuaţia (4) este neliniară, soluţia fiind de forma

,

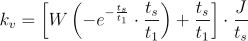în care W(a) este funcţia Lambert W. Aceasta este inversul funcţiei 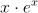, valoarea ei pentru

,

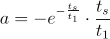rezultând ca soluţie a ecuaţiei

,

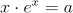ce poate fi rezolvată prin iteraţii numerice.

În final, pentru valorile determinate experimental, se obţine

k_v = 0,003262 Nms.

Cuplul de frecări uscate m_f. Se calculează direct cu relaţia (3), rezultând

m_f = 0,1 Nm.