Se consideră un circuit serie 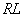 , alimentat de la o sursă de tensiune alternativă sinusoidală, descrisă de
, alimentat de la o sursă de tensiune alternativă sinusoidală, descrisă de 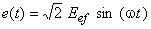 .
.

Figura 9 - Schema circuitului serie RL
Cunoscând valorile lui  şi
şi  , să se determine (vezi Circuitul RL serie) expresiile impedanţei totale a circuitului şi a curentului pe care îl absoarbe în regim permanent, considerând că faza iniţială a amplitudinii complexe a tensiunii este nulă, respectiv
, să se determine (vezi Circuitul RL serie) expresiile impedanţei totale a circuitului şi a curentului pe care îl absoarbe în regim permanent, considerând că faza iniţială a amplitudinii complexe a tensiunii este nulă, respectiv 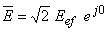 .
.
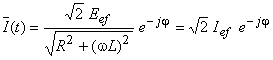 |
cu |
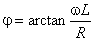 |
şi |
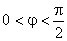 |
Puterea complexă a acestui circuit (care este puterea pe care sursa va trebui să o furnizeze pentru alimentarea circuitului), va fi dată de
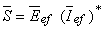
Ţinând cont de expresiile amplitudinilor complexe ale tensiunii şi curentului, puterea complexă rezultă:
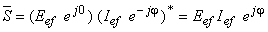
Puterile activă, reactivă şi aparentă sunt:
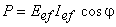
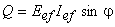
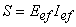
Cum 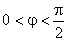 , rezultă că toate aceste puteri au valori pozitive.
, rezultă că toate aceste puteri au valori pozitive.
Cunoscând amplitudinile complexe ale tensiunilor la bornele elementelor, 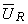 şi
şi 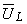 (vezi Circuitul RL serie), se pot calcula puterile în fiecare din elementele circuitului (elementul R şi elementul L).
(vezi Circuitul RL serie), se pot calcula puterile în fiecare din elementele circuitului (elementul R şi elementul L).
Ştiind că 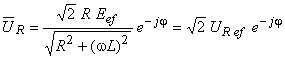 , puterea complexă asociată rezistenţei este:
, puterea complexă asociată rezistenţei este:
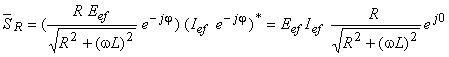
Cum 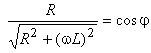 (vezi Figura 2 din Circuitul RL serie), se obţine:
(vezi Figura 2 din Circuitul RL serie), se obţine:
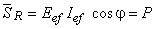
Aceasta înseamnă că puterea activă din circuit este asociată prezenţei unei rezistenţe.
În mod similar, pentru bobină avem
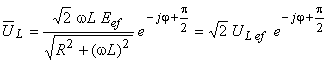 .
.
Rezultă că puterea complexă asociată bobinei este:
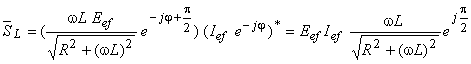
Cum 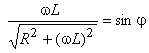 (vezi Figura 2 din Circuitul RL serie), se obţine:
(vezi Figura 2 din Circuitul RL serie), se obţine:
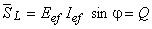
Aceasta înseamnă că puterea reactivă din circuit este asociată prezenţei bobinei.
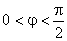 , rezultă că, impedanţa complexă este reprezentată de vector aflat în cadranul I, iar puterea activă ia valori pozitive; circuitul consumă energie reactivă de la sursa de tensiune.
, rezultă că, impedanţa complexă este reprezentată de vector aflat în cadranul I, iar puterea activă ia valori pozitive; circuitul consumă energie reactivă de la sursa de tensiune.