The conservation of the instantaneous power leads to:

the power associated to the fundamental components of each of the terms has the value:

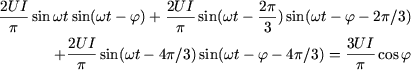We prove this equality by using the following formulas:

To this power is associated the continuous component of

The power associated to the 5^th rank harmonics of each of the voltages has the value:

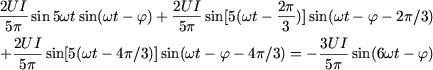The power associated to the 7^th rank harmonics of each of the voltages has the value:

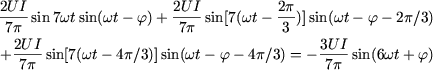The powers associated to the 5^th and 7^th rank harmonics of the voltages give the terms of the 6^th rank harmonics of the current .

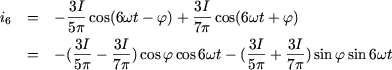In the same way the powers associated to the 11^th and 13^th rank harmonics of the voltages give the terms of the 12^th rank harmonics of the current

and so on.