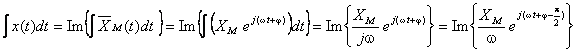Adunarea a două mărimi sinusoidale de aceeaşi pulsaţie (frecvenţă)
Fiind date două mărimi sinusoidale descrise de:
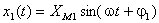 |
şi |
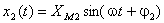 , , |
analitic, suma lor va fi dată de:
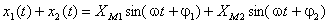 .
.
Dacă cele două mărimi se reprezintă cu ajutorul vectorilor rotitori corespunzători, suma lor va fi dată de suma celor doi vectori; evoluţia temporală a sumei, corespunde părţii imaginare a sumei vectorilor:
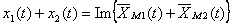
Multiplicarea unei mărimi sinusoidale cu o constantă reală
Dată fiind o mărime sinusoidală descrisă de:
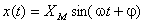 ,
,
analitic, multiplicarea sa cu o constantă reală 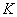 conduce la:
conduce la:
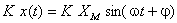
Dacă mărimea se reprezintă cu ajutorul vectorului rotitor corespunzător, multiplicarea sa cu 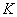 conduce la un vector colinear cu
conduce la un vector colinear cu 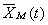 , dar al cărui modul este
, dar al cărui modul este 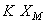 ; evoluţia temporală a semnalului
; evoluţia temporală a semnalului 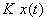 corespunde părţii imaginare a vectorului:
corespunde părţii imaginare a vectorului:
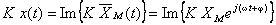
Produsul a două mărimi sinusoidale de aceeaşi pulsaţie (frecvenţă)
Fiind date două mărimi sinusoidale descrise de:
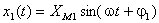 |
şi |
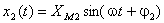 |
analitic, produsul lor este dat de:
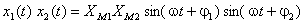
Dacă cele două mărimi se reprezintă cu ajutorul vectorilor rotitori corespunzători, produsul lor va fi reprezentat de un vector cu faza 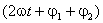 , care se roteşte cu viteză unghiulară dublă şi având modulul
, care se roteşte cu viteză unghiulară dublă şi având modulul 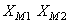 ; evoluţia temporală a produsului corespunde părţii imaginare a vectorului:
; evoluţia temporală a produsului corespunde părţii imaginare a vectorului:
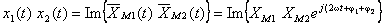
ANIMAŢIE
Derivarea unei mărimi sinusoidale
Dată fiind o mărime sinusoidală descrisă de:
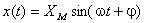 ,
,
analitic, derivata sa este dată de:
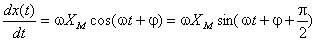
Dacă mărimea se reprezintă cu ajutorul vectorului rotitor corespunzător, derivata sa va fi reprezentată de un vector având faza 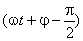 , fiind deci în avans relativ cu
, fiind deci în avans relativ cu 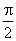 faţă de
faţă de 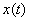 , şi modulul
, şi modulul 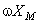 ; evoluţia temporală a derivatei corespunde părţii imaginare a vectorului:
; evoluţia temporală a derivatei corespunde părţii imaginare a vectorului:
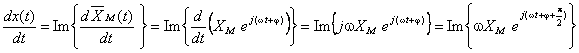
Integrarea unei mărimi sinusoidale
Dată fiind o mărime sinusoidală descrisă de:
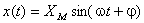
analitic, integrala sa este dată de:
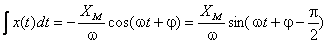
Dacă mărimea se reprezintă cu ajutorul vectorului rotitor corespunzător, integrala sa va fi reprezentată de un vector având faza 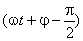 , fiind deci în urmă cu
, fiind deci în urmă cu 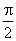 faţă de
faţă de 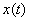 , şi modulul
, şi modulul 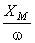 ; evoluţia temporală a integralei corespunde părţii imaginare a vectorului:
; evoluţia temporală a integralei corespunde părţii imaginare a vectorului: